今天要進入新的主題：樹（Tree）。這個結構人類一定很熟悉，基礎的目錄就是用樹的方式儲存的，生活中也有很多應用

何謂樹？

樹的定義為：

1. 由至少 1 個節點組成，不可為空。該節點稱為樹根（root）
2. 其餘節點 分為 T1 ~ Tm 個集合，稱為樹根的子樹（subtree）
3. 樹之分支無方向性

樹的相關名詞

這邊非常重要，接下來要討論有關於樹的任何主題，都會頻繁的使用到這些相關名詞
來看個範例：樹根為 A，總共有 3 個 subtree 的樹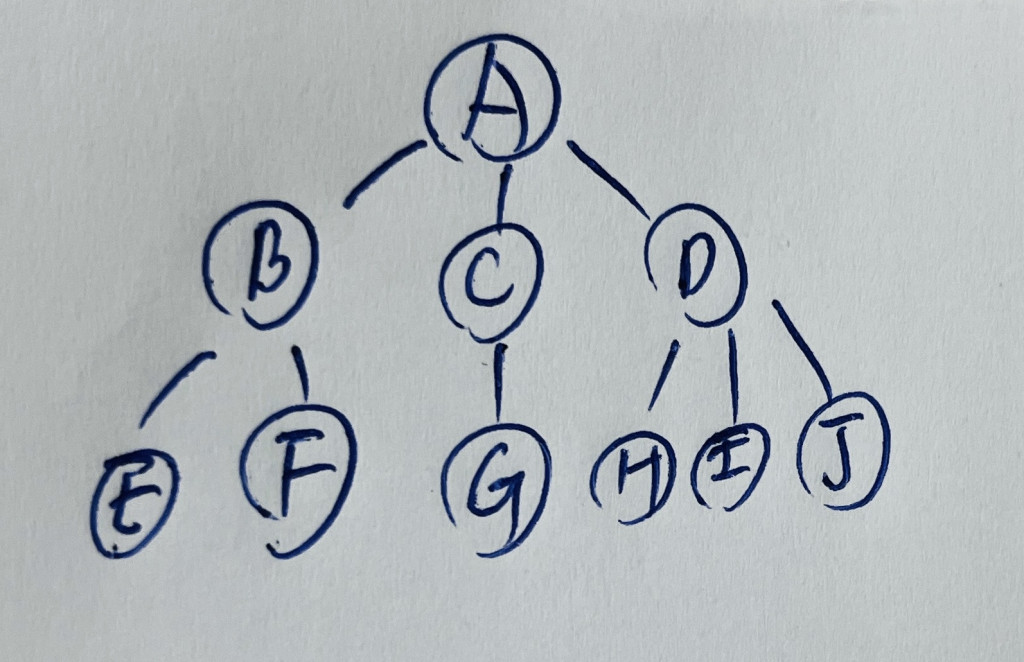

1. 節點的分支度（node's degree）：代表該節點有幾棵子樹，例如 A 的分支度為 3，B 的分支度為 2。
2. 樹葉節點（leaf）：分支度為 0 的節點。如 E F G H I J
3. 非樹葉節點（non-leaf）：A B C D
4. 父子關係（parent and child）：如 A 是 B 的 parent，B 則是 A 的 child。
5. 兄弟節點（sibling）：具有相同 parent 的節點。如 E F 互為兄弟節點。
6. 祖先與後代（ancestor and descendant）：從該點至樹根所經過之所有節點為祖先。如 G 之祖先為 C A。
   反之，該點至樹葉所經過之所有節點為後代。
7. 節點階度（level）：若 parent 之 level 值為 I，則自身 level 值為 I + 1。其中樹根之 level 值可能為 1 或 0。如假設 A 點 level 值為 1。則 C 之 level 值為 2。
8. 樹的分支度（Tree's Degree）：所有節點之 Degree 最大值。如此樹之 Degree 為 3。
9. 樹高（Height, Depth）：此樹所有節點之 level 最大值。如此樹 level 為 3。

樹的表示法

方法一：括號法

父點在括號外，括號內用逗點區隔每個子樹。
如上述之樹可表示為：A(B(E, F), C(G), D(H, I, J))

方法二：直接使用 Linked List 表示

先來定義節點結構：一個位置存資料，後面的欄位階保留給鏈結使用，作為樹的分支指向 child node。

例如，剛剛的樹可以表示成這樣：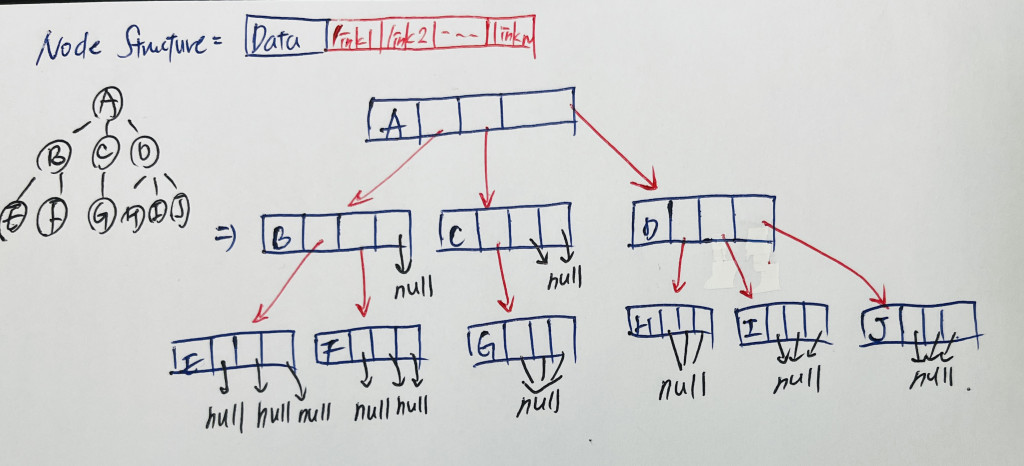

看似相當的容易理解，但這有個大問題：
極度浪費 Linking Space
假設這棵樹的 degree 為 K，代表節點結構中必須要有 K 個 space 來儲存鏈結。又假設總共有 N 個節點，那麼整棵樹需要配置的鏈結空間為 NK 個。不過，實際用到的只有 N - 1 個，因為除了 root 之外，所有節點皆被一個鏈結連接。所以浪費了：NK - (N - 1) = N(K - 1) - 1 個空間。
比方說上面那棵樹，就浪費了：3 * 10 - (10 - 1) = 21 個空間。
看起來還好，計算一下比例：(N - 1) / N(K - 1) - 1，浪費趨近於 (K - 1) / K，如果這個 Tree 的 degree 是 10，那其浪費了 90% 的空間。太浪費了！

因次我們想將這個浪費的比例降到最低，Tree Degree 為 2 的話，可以將其精簡至浪費 1 / 2。

所以 明天我們就來討論一個新的結構：二元樹（Binary Tree）